Парадигма платформы Miracle.
Технология, положенная в основу работы платформы Miracle, базируется на принципах
формирования модели решения. Где структура решения является системой объектов из имеющегося множества. При этом один и
тот же объект может встречаться несколько раз. Структура решения может иметь большое количество отдельных и
взаимозависимых систем, являющиеся компонентами единой сети.
Основой проектируемой сети является условно-событийное понятие системы. Компоненты системы и их
действия представляются «событиями». Событие может произойти (реализоваться) единожды, многократно или не разу.
Совокупность действий, возникающих как реализация событий при функционировании системы, формирует «процесс». При
этом система может функционировать по разному в одних и тех же условиях, порождая множество «процессов». Для того, что
бы событие произошло, необходимо появление «ситуации», в которой это событие может быть реализовано. Ситуация
возникновения события определяется совокупностью некоторых «условий» способствующих поддержанию процесса.
Множество процессов порождаемые событиями, возникающие как следствие появления ситуаций при формировании
соответствующих условий, поддерживают общее функционирование «условно-событийной» системы.
В условно-событийной системе «условия» и «событие» имеют зависимые отношения, обеспечивающие
общую динамику поведения моделируемой системы. Т.е. работу системы можно представить как совокупность реализации
событий.
Данный метод является фундаментом в представленной информационной технологии, позволяющий
ориентироваться на модель решения. Математической основой данной парадигмы является формальная теория сетей Петри.
Сеть Петри - это набор PN = (P, T, F, M0), где (P, T, F) - конечная сеть
(множества P и T конечны), а М0 - функция начальной разметка сети, которая сопоставляет любому
месту pi 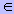 P некоторое число M0(p)= n. P некоторое число M0(p)= n.
Сеть Петри определяется как двудольный граф. Т.е. все вершины графа относятся к одному из двух
классов - позициям и переходам. Позиции соответствуют «условиям», переходы – «событиям». Последовательное
срабатывание переходов и соответствующее изменение разметки сети называют процессом функционирования сети.
Функционирование сети Петри описывается формально с помощью множества последовательностей
срабатываний и множества достижимых в сети разметок. Эти понятия определяются через правила
срабатывания переходов сети.
Разметка сети PN является функцией M : P
 N (здесь N - множество натуральных чисел). Если предположить, что
все места сети строго упорядочены каким-либо образом, т.е. P = ( p1, p2, ...pn), то разметку M
сети (в том числе и начальную разметку) можно задать как вектор чисел M = (m1, m2,... mn) такой, что
для любого i, 1 N (здесь N - множество натуральных чисел). Если предположить, что
все места сети строго упорядочены каким-либо образом, т.е. P = ( p1, p2, ...pn), то разметку M
сети (в том числе и начальную разметку) можно задать как вектор чисел M = (m1, m2,... mn) такой, что
для любого i, 1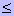 i i 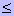 n mi = M(pi).
Если P' = {pi1, pi2, ...pik) - подмножество мест из P, то условимся через M(P') обозначать
множество разметок {M(pi1),...M(pik)}. Если P' представить как вектор
P' = (pi1, ... pik), то M(P') обозначает вектор проекции разметки M на P'. n mi = M(pi).
Если P' = {pi1, pi2, ...pik) - подмножество мест из P, то условимся через M(P') обозначать
множество разметок {M(pi1),...M(pik)}. Если P' представить как вектор
P' = (pi1, ... pik), то M(P') обозначает вектор проекции разметки M на P'.
Переход t может сработать при некоторой разметке M сети PN, если
 p p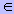 *t M(p) *t M(p)
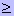 F (p,t), то есть каждое входное место p перехода t имеет разметку, не меньшую, чем кратность дуги, соединяющей p и t.
Это условие можно переписать в векторной форме следующим образом:
F (p,t), то есть каждое входное место p перехода t имеет разметку, не меньшую, чем кратность дуги, соединяющей p и t.
Это условие можно переписать в векторной форме следующим образом:
M 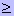 *F (p,t). *F (p,t).
Для ординарной сети Петри (то есть сети, в которой дуги имеют
кратность, равную единице) условие срабатывания перехода означает, что любое
входное место этого перехода содержит хотя бы один маркер, то есть имеет
ненулевую разметку. Срабатывание перехода t при разметке M порождает разметку M' по следующему правилу:
 p p 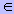 P : M'(p) = M(p) - F (p,t) + F (t,p) , то есть M' = M - *F(t) + F*(t).
P : M'(p) = M(p) - F (p,t) + F (t,p) , то есть M' = M - *F(t) + F*(t).
На множестве разметок вводят отношение [ > непосредственного следования разметок:
M [ > M'  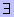 t t
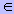 T : (M T : (M 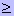 *F(t)) & (M' = M - *F(t) + F*(t)), то есть разметка M' непосредственно следует за разметкой M, если найдется такой переход t,
который может сработать при разметке M и разметка M' является результатом срабатывания этого перехода при
разметке M.
*F(t)) & (M' = M - *F(t) + F*(t)), то есть разметка M' непосредственно следует за разметкой M, если найдется такой переход t,
который может сработать при разметке M и разметка M' является результатом срабатывания этого перехода при
разметке M.
Говорят, что разметка M' достижима от разметки M, если существует последовательность разметок M, M1,
M2, ...M' и слово 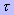 = t1t2......tk в алфавите T такие, что M[t1 > M1[t2>
M2.....[tk> M'. = t1t2......tk в алфавите T такие, что M[t1 > M1[t2>
M2.....[tk> M'.
Слово 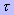 в этом случае называется последовательностью
срабатываний, ведущих от M к M'. в этом случае называется последовательностью
срабатываний, ведущих от M к M'.
Множество разметок, достижимых в сети PN от разметки M, обозначим через R(PN,M).
Множество R(PN) = R(PN,M0), то есть множество всех разметок, достижимых в сети PN от начальной разметки
M0, называют множеством достижимых разметок сети.
© Москва 2001г. НПФ "И.В.А." Горшков В.А.
Перейти в раздел "Публикации"
|
